Matemáticas 2. Imaginación Espacial y Ecuaciones
Ficha de Anáisis Exponencial - Profr. Cesar Olivas
Ingresa a la siguiente Interactividad Recurso de Enciclomedia Cubicula y responde a las cuestiones solicitadas por el Profr. C. Olivas
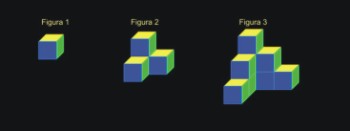
- Observen, a partir de la Imagen que en la figura 1 es posible ver tres caras del cubo, y que en la figura 2 se pueden ver nueve caras de los cubos que lo forman. ¿Cuàntas caras es posible ver en la figura 3? ¿Cuàntas en la figura 4?
- Si se continùa con la contrucciòn de las figuras, ¿cuàntas caras serìa posible ver en la figura que ocupe el lugar 15?
- Entonces, cuàl serìa la expresiòn algebraica que determine el nùmero de caras de cualquier figura en la sucesiòn.
- ¿Què nùmero de caras corresponde en la sucesiòn de la figura 153?
23 comentarios
GERARDO -
esta formula la obtuve através de la deducción de números sucesorios
la figura 1 tiene 3 caras
la figura 2 tiene 9 caras
la figura 3 tiene 17 caras
por tanto:
la figura 15 tendra 179 caras
y la figura 153 tendra 23867
Andrea Acosta -
Figura 1- 3x1=3
Figura 2- 9x1=9
Figura 3- 9x2=18
Figura 4- 9x3=27
o que va aumentado 2 en cada base.
karla daniela lopez flores -
Andrea Ramírez -
Andrea Ramírez: bueno observe que las figuras es decir los cubos tienen un seguimiento o secuencia que se va sumando, multiplicando con los múltiplos de 3 por que son el numero de caras que se pueden observar en la primera figura geométrica el cubo, entonces en la segunda figura se miran 9 caras de las cuales son de la figura numero 2 yen la figura numero 3, la siguiente, se observa el doble de caras que la anterior (18); y así sucesivamente 9*2= 18caras que se observan. Esta fue la conclusión.
ANDREA VELEZ RIOS -
Ismael Alberto Moncada Ramírez, y Erick Ashley Loera Castillo -
Angelica y Lakshmy -
Lo resolvimos viendo las caras de cada cubo y sumando las correspondientes.
Lakshmy y Angelica
bye profe..
Ismael Alberto Moncada Ramírez, y Erick Ashley Loera Castillo -
Cuauhtemoc Silva Rios -
Ivan Villamnueva,Ramon Rosas -
miriam y eduardo -
Erik Montiel Chaidez -
Christian mejorado maldonado, Jose luis urban Martinez -
Alejandra Gómez Barrientos & Alejandra martínez arrieta -
la direncia en 9 y 3 es 6
la diferencia entre 17 y 9 es 8
y asi se podría sacar el resto de los números
jesus de busk , sara karen -
Abril Arreola y Mariazell Alcázar -
En la figura 15 se verian mas o menos como 439 caras.
Entonces la expresion algebraica seria como
(x)(y)= 439
Y en la figura 153 serian como 67,167 caras visibles.
Wendy Teresita Bonilla Moreno y Ana Paulina Torres Franco -
17 caras 27 caras 39 caras.
Figura #15 Figura #153
117 caras 1187 caras
Para llegar a estas conclusiones tuvimos que hacer varias operaciones y la formula que utilizamos fue:
c (3)= x
samantha y miroslava coral -
Daniel Pereda y Felipe Raygoza -
La figura 4 la sacamos de por lógica y porque todo se sube al cubo
R0bErTo y JoNtHan -
jose luis, christian ivan -
en la de 153 son 918
Jose luis, Christia ivan -
en la figura 4 son 27
en la figura 5 son 36
chritian Josè -